Authors: Max Rossmannek, Panagiotis Kl. Barkoutsos, Pauline J. Ollitrault, and Ivano Tavernelli
Title: “Quantum HF/DFT-embedding algorithms for electronic structure calculations: Scaling up to complex molecular systems”
Journal: The Journal of Chemical Physics 154, 114105
Year: 2021
The Schrödinger equation is one of the fundamental equations which helps us understand, among other things, how the electrons behave in a molecule. The goal in the scientific field is to solve the Schrödinger equation to obtain a specific wave function to describe an object’s full quantum configuration or state mathematically. This equation is a potent tool that theoretically allows us to calculate all the other molecular properties of the system, such as molecular geometry, energies, spectra, dipole moments, and many more. However, calculating all the properties of a complex system leads to an exponential number of possibilities that become difficult to calculate even with the world’s best supercomputers. This is especially true in cases when electrons become “highly correlated,” i.e., they start influencing each other intensely. Also, it becomes difficult for many-electron atoms or molecules to find exact solutions to the system due to the interactions between more than two bodies. This problem is similar to the many-body problem in classical mechanics. Therefore, the exact solution for the many-electron atoms or molecules with more than 2-3 atoms doesn’t exist.
Quantum computing is, in that regard, a promising resource. Quantum computers, unlike classical computers, make use of the complex “spooky” phenomenon of quantum mechanics (quantum entanglement and superposition) to solve problems, which even today’s most powerful supercomputer could never solve. In a recent paper, a team of researchers at IBM Zurich, led by Ivano Tavernelli, has successfully improved computation by combining two approximation methods with quantum computing. The strengths of each approach make up for the weaknesses in the others.
In their research, Tavernelli and coworkers used Qiskit (a computer software used for computational processing) to successfully implement two approximation methods known as Hartree-Fock (HF) theory and Density-Functional Theory (DFT) with quantum computing. While both of these approximation methods aim to solve the Schrodinger equation, they do so in different levels of detail. HF theory approximates each electron’s motion and treats the effect of all the electrons as a smeared out, average electrostatic field to calculate the total molecular wave function of the system. However, the motion of electrons in an actual molecule is much more complicated than this depiction because electrons are “correlated” in their movement, meaning they are more effective in avoiding each other. Therefore, HF isn’t able to treat electron correlation properly, which allows scope for further improvement.
Density functional theory DFT is an attempt at this improvement. While HF is based on the wave function approach, DFT is based on electron probability density, but both aim to solve the Schrödinger equation. Unlike the wave function, the electron density is measurable from experiments such as X-ray diffraction or electron diffraction. It is also more comprehensible when compared to the wave function approach. To understand the difference in complexity between the two systems, let’s take the example of a water molecule that contains ten electrons, eight electrons from the oxygen atom, and one from each hydrogen atom. The HF wave function for just one water molecule would be composed of 40 variables: three-position coordinates (x,y,z) for each electron and the fourth coordinate for each electron describing its spin. While no matter how big a system is, the electron density of the whole molecule will only depend on three position variables. Therefore, to deal with larger molecules, DFT is mathematically more feasible. DFT is routinely used on classical computers. However, Tavernelli’s group is the first one to use DFT embedding in combination with quantum computers.
To take the potential advantage of the available quantum algorithm, only a portion of the full system is computed using a high-level quantum computing approach, while the rest is traded with an efficient but approximate electronic structure method such as HF or DFT. The idea of this scheme is to divide a more extensive molecular system into smaller tractable parts.
The system is divided into an “active space” composed of the small set of electrons directly involved in the chemical reaction, calculated by quantum computing, and an inactive space consisting of everything else that HF or DFT estimates. Active orbitals feel the presence of inactive electrons of the environment, whose calculation is outsourced to classical HF or DFT framework. Thoughtfully partitioning the system allows the use of fewer computational resources at a good level of accuracy. Figure 1 shows the distinction between active and inactive spaces.
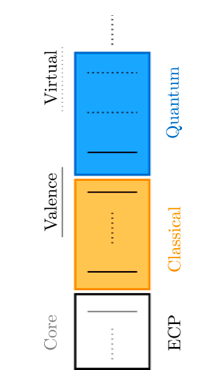
This work introduced a DFT embedding scheme. Here, a classical computer performs a DFT calculation for a full system and provides an initial density and the one and two-electron integral terms. (These terms are present in the mathematical expression of total electronic energy of the system). This density is then divided into active and inactive parts. Also, the two-electron integrals are split into long-range and short-range components. This is necessary to avoid doubling the counting of electron correlation terms. These parameters are adjusted until the density of the system is minimised. The Variational Quantum Eigensolver (VQE) algorithm is used, which runs partly on a classical computer and partly on a quantum computer. For a given “guess” density, VQE uses the quantum computer to evaluate its energy, while it uses the classical computer to choose these parameters to further lower this energy. This process is iterated until the result convergences, which is very close to exact ground state energy
After developing their computer code, Tavernelli and coworkers tested its performance on molecular systems. The most notable achievement of this approach was a remarkable accuracy for strongly correlated nitrogen molecules. These results will improve ammonia production, which is widely used in fertilizer industries using the Haber-Bosch process. Also, the DFT scheme was tested on the oxirane molecule, a system too big to be solved by state-of-the-art quantum computers, and gave promising results. This scheme is an excellent first step to further carry out electronic structure calculations for larger molecular systems using quantum computing. This will enable HF and DFT embedding schemes to make quantum computing possible for solving essential questions, which remain beyond the scope of classical computers and will lead to discoveries. It has potential applications in many fields such as chemistry, drug discovery, strongly correlated systems, field theory, material science, and many others.